$Manacher$ | 学习笔记

$Manacher$ 回文字符串匹配

应用：求最长回文串长度

基本思想

由于当 $P_i$ 存储回文字符串长度时 需要找出字符串中轴，因此需要将偶数位数的回文串对应到一个有奇数位数的回文串。我们可以在字符串的两两字母之间用一个没有出现过的字符 # 隔开，同时为了更加方便地处理边界问题，可在字符串开头加 $，末尾加 ^ [^1]

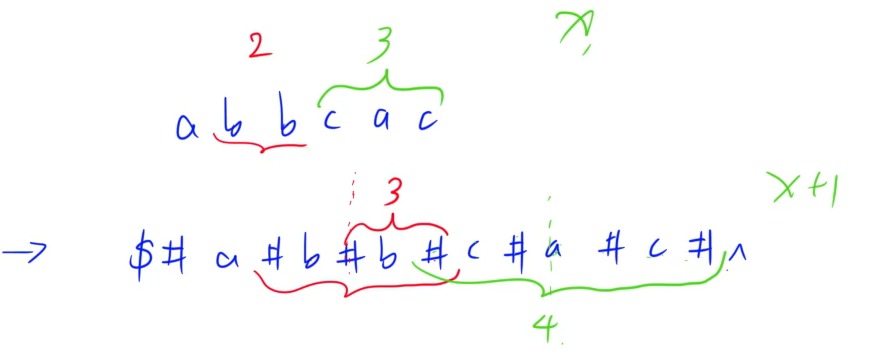
由此可以发现，原回文串长度等于新回文串的半径（包括中心点），因此仅需计算出新回文串的最大长度即可

我们设 $P_i$ 表示以 $S_i$ 为中心的最大回文串长度的半径（含 $S_i$）
动态维护一个当前计算完的最长回文串，设这个回文串的中心位置为 $mid$，最大右边界 $mr$，通过这个最大右边界更新下一个位置 $i$ 的最长回文串

依据 $i$ 与 $mr$ 的相对位置，可以分为以下两种情况

1. $i$ 在 $mr$ 左侧：
   
   找到 $i$ 相对于 $mid$ 的对称点 $j$，（$j = 2 \times mid - i$），再根据 $P_j$ 的值分为以下两类：

   1. $P_j$ 未超过左边界，直接更新 $P_i = P_j$（左右两侧字符完全相同）
   2. $P_j$ 超过了左边界. 然而可以发现 $P_i$ 一定不会超过左边界. 如果 $P_i$ 超过左边界，会推出一个更长的回文字符串 $P_j$，与已知条件矛盾。此时更新为 $p_i = mr - i$ 即可
      

   因此转移为：

   $$P_i = \min(P_j,\ mr - i)$$

   再向外暴力枚举判断是否相同即可. 因此有 $P_i \geqslant (P_j, mr - i)$

2. $i$ 在 $mr$ 右侧：
   将 $P_i$ 赋值为 $1$，暴力向外枚举.

while (s[i - p[i]] == s[i + p[i]]) p[i] ++;

最后，使用新计算的 $P_i$ 更新 $mr$

if (i + p[i] > mr) mr = i + f[i], mid = i;

时间复杂度 $O(n)$ 证明

可以发现当 $P_j$ 左侧恰好取到左边界时，$P_i$ 才需要更新，而右端点是单调递增且严格小于等于 $n$ 的，因此总时间复杂度为 $O(n)$

模板

注意匹配串 $s$ 需要开二倍数组空间，以存放特殊字符信息

int n;
// refers to the length of strings
int p[N << 1];
// used to store the longest palindrome string length
char input[N], s[N << 1];
// input strings and changed strings

经过以下操作，$P_i$ 中存储了最长回文串半径（包含中心点），答案即为 $p_i - 1$

void Manacher() {
	int mid = 0, mr = 0;
	for (int i = 1; i < n; ++ i) {
		p[i] = i < mr ? min(p[(mid << 1) - i], mr - i) : 1;
		while (s[i - p[i]] == s[i + p[i]]) p[i] ++;
		if (i + p[i] > mr) mr = i + p[i], mid = i;
	}
}

如需在 $P_i$ 中存储最长回文串长度，在字符之间插入占位字符即可

int init() {
// 返回新字符串长度 
	int idx = 0;
	s[idx ++] = '$', s[idx ++] = '#';
	for (int i = 0; i < n; i ++)
		s[idx ++] = input[i], s[idx ++] = '#';
	s[idx ++] = '^';
	return idx;
}

在此之后，$p_i - 1$ 表示以 $i$ 为中心点的最长回文串长度

例题

1. $THUPC\ 2018$ - 绿绿和串串

[^1]:$ 表示字符串开头，^ 表示字符串结尾的结尾，这种命名方式在正则表达式中广泛应用